sin2x + cos2x = 0
sin2x + cos2x = 0
=> √2.sin(2x + π/4) = 0
=> sin(2x + π/4) = 0
=> 2x + π/4 = kπ
=> 2x = -π/4 + kπ
=> x = – π/8 + kπ/2 (k € Z)
sin2x+cos2x+1=0
Do sin2x+cos2x>=0 nên Phương trình vô nghiệm.
Trong lượng giác, sin, cos và tan là các tỷ số lượng giác cơ bản được sử dụng để nghiên cứu mối quan hệ giữa các góc và các cạnh của một tam giác (đặc biệt là của một tam giác vuông). Pythagoras nghiên cứu mối quan hệ giữa các cạnh của tam giác vuông thông qua định lý Pitago trong khi Hipparcus nghiên cứu về việc thiết lập mối quan hệ giữa các cạnh và góc của một tam giác vuông bằng cách sử dụng các khái niệm lượng giác. Các công thức sin, cos và tan trong lượng giác được sử dụng để tìm các cạnh hoặc góc bị thiếu của một tam giác vuông.
Hãy hiểu sin, cos và tan trong lượng giác bằng cách sử dụng các công thức và ví dụ.
Sin Cos Tan trong Lượng giác là gì?
Sin, cos và tan là ba tỉ số lượng giác cơ bản, lần lượt là sin, cosin và tiếp tuyến, trong đó mỗi tỉ số cho biết tỉ số hai cạnh của một tam giác vuông. Chúng ta biết rằng cạnh dài nhất của một tam giác vuông được gọi là “cạnh huyền” và hai cạnh còn lại được gọi là “chân”. Điều đó có nghĩa là, trong lượng giác, cạnh dài nhất của tam giác vuông vẫn được gọi là “cạnh huyền” nhưng hai chân còn lại được đặt tên là:
phía đối diện
bên cạnh
Chúng tôi quyết định các mặt “đối diện” và “liền kề” dựa trên góc mà chúng ta đang nói đến.
“Mặt đối diện” hay mặt vuông góc là mặt vừa “đối diện” với góc.
“Cạnh kề” hoặc cơ sở là mặt (không phải cạnh huyền) “tiếp xúc” với góc.
Giá trị Sin Cos Tan
Các giá trị Sin, Cos và Tan trong lượng giác đề cập đến các giá trị của hàm lượng giác tương ứng đối với góc đã cho. Chúng ta có thể tìm các giá trị sin, cos và tan của một tam giác vuông đã cho bằng cách tìm tỉ số các cạnh cần thiết. Hãy cùng chúng tôi tìm hiểu các công thức để tìm các tỷ lệ này một cách chi tiết trong các phần sau.
Công thức Sin Cos Tan
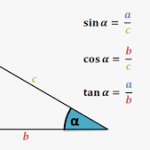
Các hàm sin, cos và tan trong lượng giác được xác định theo hai trong ba cạnh (đối diện, cạnh kề và cạnh huyền) của một tam giác vuông. Dưới đây là công thức của sin, cos và tan.
sin= cạnh đối/ cạnh huyền
cos= cạnh kề/ cạnh huyền
tan= cạnh đối/ cạnh kề
cot= cạnh kề/ cạnh đối
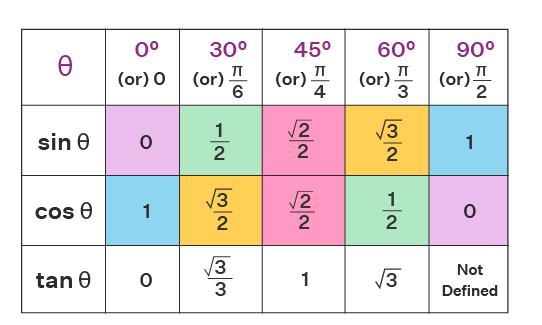
Bảng Sin Cos Tan
Các tỷ số lượng giác, sin, cos và tan không hoàn toàn phụ thuộc vào độ dài các cạnh của tam giác mà chúng phụ thuộc vào góc bởi vì cuối cùng, chúng ta đang lấy tỷ số của các cạnh. Bảng sin, cos và tan được sử dụng để tìm giá trị của các hàm lượng giác này đối với các góc chuẩn. Trong quá trình tính toán liên quan đến tỷ số sin, côsin hoặc tiếp tuyến, chúng ta có thể tham khảo trực tiếp biểu đồ trig được đưa ra trong phần sau để thực hiện các suy luận dễ dàng hơn.