Giải: Cho tập hợp A = {a; b; c; d; e; f}. Số tập hợp con của tập hợp A là: A. 6 B. 12 C. 64 D. 32

Giải: Cho tập hợp A = {a; b; c; d; e; f}. Số tập hợp con của tập hợp A là:

A. 6

B. 12

C. 64

D. 32

Số tập con của A là 2^6 và bằng 64. Vậy đáp án đúng là C.

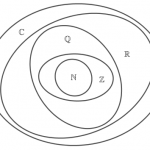
Trong toán học, tập hợp A là tập con của tập hợp B nếu tất cả các phần tử của A cũng là phần tử của B; Khi đó B là một tập siêu của A. Có thể cho A và B bằng nhau; nếu chúng không bằng nhau, thì A là một tập hợp con thích hợp của B.

Mối quan hệ của một tập hợp này với tập hợp con của tập hợp khác được gọi là bao hàm (hoặc đôi khi bao hàm). A là một tập con của B cũng có thể được biểu thị là B bao gồm (hoặc chứa) A hoặc A được bao gồm (hoặc chứa) trong B.

Quan hệ tập hợp con xác định thứ tự từng phần trên các tập hợp. Trên thực tế, các tập con của một tập hợp đã cho tạo thành đại số Boolean dưới quan hệ tập hợp con, trong đó phép nối và sự gặp nhau được cho bởi giao và sự kết hợp, và bản thân quan hệ tập hợp con là quan hệ bao hàm Boolean.

Trong toán học và logic, bất kỳ tập hợp nào của các đối tượng (phần tử), có thể là toán học (ví dụ: số, hàm) hoặc không. Ý tưởng trực quan về một tập hợp có lẽ thậm chí còn cũ hơn so với ý tưởng về số lượng. Ví dụ, các thành viên của một đàn động vật có thể được ghép với các viên đá trong một bao tải mà không cần các thành viên của một trong hai tập hợp thực sự được đếm.

Ý niệm mở rộng vào cái vô hạn. Ví dụ, tập hợp các số nguyên từ 1 đến 100 là hữu hạn, trong khi tập hợp tất cả các số nguyên là vô hạn. Một tập hợp thường được biểu diễn dưới dạng danh sách tất cả các thành viên của nó được đặt trong dấu ngoặc nhọn.

Một tập hợp không có thành viên nào được gọi là tập hợp rỗng, hoặc rỗng, và được ký hiệu là ∅. Bởi vì một tập hợp vô hạn không thể được liệt kê, nó thường được biểu diễn bằng một công thức tạo ra các phần tử của nó khi áp dụng cho các phần tử của tập hợp số đếm. Do đó, {2x | x = 1,2,3, …} đại diện cho tập hợp các số chẵn dương (thanh dọc có nghĩa là “sao cho”).

Nếu mọi phần tử của tập A cũng thuộc B, thì A được mô tả là một tập con của B hoặc chứa trong B, được viết A ⊆ B, [37] hoặc B ⊇ A. Kí hiệu thứ hai có thể được đọc là B chứa A, B bao gồm A, hoặc B là một tập hợp con của A. Mối quan hệ giữa các tập hợp được thiết lập bởi ⊆ được gọi là bao hàm hoặc bao hàm. Hai tập hợp bằng nhau nếu chúng chứa nhau: A ⊆ B và B ⊆ A tương đương với A = B.

Nếu A là một tập con của B, nhưng A không bằng B, thì A được gọi là một tập con thích hợp của B. Điều này có thể được viết A ⊊ B. Tương tự như vậy, B ⊋ A có nghĩa là B là một tập hợp con thích hợp của A, tức là B chứa A, và không bằng A.

Cặp toán tử thứ ba ⊂ và ⊃ được các tác giả khác nhau sử dụng theo cách khác nhau: một số tác giả sử dụng A ⊂ B và B ⊃ A để có nghĩa là A là bất kỳ tập con nào của B (và không nhất thiết phải là tập con thích hợp), trong khi những người khác dành A ⊂ B và B ⊃ A cho các trường hợp A là một tập hợp con thích hợp của B.