Cho tập hợp X = {1; 2; 3; 4}. Câu nào sau đây đúng? A. Số tập con của X là 14 ; B. Số tập con của X gồm có 4 phần tử là 1; C. Số tập con có 1 phần tử là 5; D. Số tập con có chứa phần tử 1 là 6.

Cho tập hợp X = {1; 2; 3; 4}. Câu nào sau đây đúng? A. Số tập con của X là 14 ; B. Số tập con của X gồm có 4 phần tử là 1; C. Số tập con có 1 phần tử là 5; D. Số tập con có chứa phần tử 1 là 6.

A. Số tập con của X là 14. Sai vì số tập con của X là 2^4= 16

B. Số tập con của X gồm có 4 phần tử là 1. Đúng {1; 2; 3; 4}

C. Số tập con có 1 phần tử là 5. Sai vì phải là 4 tập con : {1}; {2}; {3}; {4}

D. Số tập con có chứa phần tử 1 là 6. Sai vì có 7 tập con: {1}; {1; 2}; {1; 3}; {1; 4}; {1; 2; 3}; {1; 3; 4}; {1; 2; 3; 4}

Vậy đáp án đúng là B.

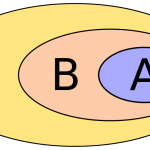
Trong toán học, tập hợp A là tập con của tập hợp B nếu tất cả các phần tử của A cũng là phần tử của B; Khi đó B là một tập siêu của A. Có thể cho A và B bằng nhau; nếu chúng không bằng nhau, thì A là một tập hợp con thích hợp của B. Mối quan hệ của một tập hợp này với tập hợp con của tập hợp khác được gọi là bao hàm (hoặc đôi khi bao hàm). A là một tập con của B cũng có thể được biểu thị là B bao gồm (hoặc chứa) A hoặc A được bao gồm (hoặc chứa) trong B.

Quan hệ tập hợp con xác định thứ tự từng phần trên các tập hợp. Trên thực tế, các tập con của một tập hợp nhất định tạo thành đại số Boolean dưới quan hệ tập hợp con, trong đó phép nối và sự gặp nhau được cho bởi giao và sự kết hợp, và bản thân quan hệ tập hợp con là quan hệ bao hàm Boolean.

Tập hợp là những tập hợp được xác định rõ ràng và hoàn toàn được đặc trưng bởi các phần tử của chúng. Do đó, hai tập hợp là bằng nhau nếu và chỉ khi chúng có chính xác các phần tử giống nhau. Mối quan hệ cơ bản trong lý thuyết tập hợp là mối quan hệ của phần tử, hoặc phần tử. Ta viết a∈A để chỉ ra rằng đối tượng a là một phần tử hay một phần tử của tập A. Ta cũng nói rằng a thuộc A. Như vậy, tập A bằng tập B nếu và chỉ khi với mọi a, a∈A nếu và chỉ khi a∈B. Đặc biệt, chỉ có một tập hợp không có phần tử nào cả. Tập hợp này tự nhiên được gọi là tập hợp rỗng, và được biểu thị bằng ký hiệu ∅.

Ta nói rằng A là một tập con của B, được viết A⊆B, nếu mọi phần tử của A là một phần tử của B. Như vậy, A = B nếu và chỉ khi A⊆B và B⊆A. Chú ý rằng ∅⊆A, với mọi tập hợp A.

Cho các tập hợp A và B, người ta có thể thực hiện một số phép toán cơ bản với chúng để tạo ra các tập hợp sau:

Tập hợp A∪B, được gọi là hợp của A và B, có phần tử là phần tử của A và phần tử của B.

Tập hợp A∩B, được gọi là giao điểm của A và B, có phần tử là phần tử chung của A và B.

Tập hợp A − B, được gọi là hiệu của A và B, có các phần tử là các phần tử của A mà không phải là phần tử của B.