Phương pháp giải tìm giới hạn hàm số dạng âm vô cùng nhân với 0 bằng bao nhiêu

Có những phương pháp tìm giới hạn hàm số nào? Bài viết ngày hôm nay, chúng tôi xin chia sẻ tới các bạn phương pháp giải tìm giới hạn hàm số dạng âm vô cùng nhân với 0 bằng bao nhiêu.

Phương pháp giải tìm giới hạn hàm số dạng âm vô cùng nhân với 0 bằng bao nhiêu

1, Hai giới hạn quan trọng

Đứng đầu tiên dĩ nhiên là hai giới hạn quan trọng mà bạn bắt buộc phải ghi nhớ:

(1)

(2)

2, Thay thế tương đương

Thay thế tương đương hay còn gọi là thay thế âm vô cùng tương đương. Cách thay thế thường dùng cụ thể như sau:

Khi x gần với 0, có:

(1), sinx ~ x, tanx ~ x, arcsinx ~ x, arctanx ~ x

(2), 1 – cosx ~ (1/2)x^2,  a^x – 1 ~ xlna, e^x-1 ~ x

(3), ln(1 + x) ~ x , (1 + x)^a-1 ~ ax

Trong đó chỉ cần lưu ý hai điều là được:

(1), Phép thay thế âm vô cùng tương đương chỉ được sử dụng trong phép nhân và phép chia.

(2), Có thể thay thế toàn bộ, chẳng hạn như (1 + 3x) ^ a-1 ~ 3ax

Chỉ cần bạn thành thạo trong việc sử dụng các phép thay thế âm vô cùng tương đương, các biểu thức thường trở nên rất ngắn gọn. Chúng ta hãy xem xét hai câu hỏi mẫu.

Phương pháp giải tìm giới hạn hàm số dạng âm vô cùng nhân với 0 bằng bao nhiêu

3, Âm vô cùng nhân với một số có giới hạn bằng âm vô cùng

Quy tắc này mặc dù đơn giản, nhưng nhiều người khi giải bài tập thường lãng quên.

Ví dụ: Tìm giới hạn

Khi x tiến gần tới âm vô cùng, 1/x là âm vô cùng, sin3x là số có giới hạn (không lớn hơn 1), do vậy, giới hạn của hàm số này là 0.

>> Tổng hợp đầy đủ các dạng toán về hàm hợp (toán học)

4, Quy tắc l’Hôpital

Quy tắc l’Hôpital chủ yếu có hai dạng 0/0 và ∞/∞.

Ví dụ: tìm giới hạn

Phân tích: Áp dụng quy tắc l’Hôpital để tìm giới hạn, thuộc dạng 0/0. Cụ thể:

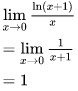
Phương pháp giải tìm giới hạn hàm số dạng âm vô cùng nhân với 0 bằng bao nhiêu

5, Định lý kẹp

Nếu yn < xn < zn và giới hạn của yn và zn đều là a thì giới hạn của xn cũng là a. Điều này cũng áp dụng cho giới hạn của hàm số. Nếu h (x) < f (x) < g (x) và giới hạn h (x) và g (x) đều là a. Thì giới hạn f (x) cũng là a . Nói một cách nôm na, nó có nghĩa là “hai bên kẹp ở giữa”. Điều quan trọng là tìm y và z hoặc h và g ở cả hai bên.

6, Định lý hội tụ có giới hạn đơn điệu

Trong các bài tập tính toán, định lý hội tụ có giới hạn đơn điệu không được sử dụng nhiều. Nhưng nếu có gặp, vì sử dụng ít nên dễ khiến người khác không nhớ ra. Do vậy, tốt nhất nên ghi ngờ, lúc nào cũng nhắc nhở bản thân có tồn tại định lý này.

Định lý hội tụ có giới hạn đơn điệu là chỉ dãy số hội tụ đơn điệu có giới hạn bắt buộc phải có giới hạn. Đối với hàm số cũng như vậy. Các quá trình tiếp cận đơn điệu và tiếp cận có giới hạn cũng phải có giới hạn.

Thực tế, bằng trực giác, chúng ta dễ dàng cảm nhận rằng xn là một dãy số có giới hạn nhỏ hơn 2. Sau đó, chúng ta chỉ cần chứng minh điều đó là được. Sử dụng phương pháp quy nạp trong toán học.

Lưu ý: Thông thường để có được một dãy số công thức truy hồi, thì phải xem xét tới định lý hội tụ có giới hạn đơn điệu.