Biểu thức tính chu vi hình vuông (và công thức tính diện tích hình Vuông)

Chu vi của một hình phẳng là độ dài của hình tròn bên ngoài của nó, nghĩa là tổng độ dài các cạnh. Theo định nghĩa, hình vuông là tứ giác có bốn cạnh bằng nhau và bốn góc vuông. Vì bốn cạnh đều có độ dài bằng nhau nên việc tính chu vi hình vuông là một vấn đề đơn giản.

Bài viết này trước hết sẽ giới thiệu phương pháp tính chu vi hình vuông thông thường sau đó là phương pháp tính chu vi hình vuông nội tiếp hình tròn có bán kính là phương pháp vòng tròn.

Phương pháp tính chu vi hình vuông khi biết độ dài của một cạnh.

Bước 1: Nhớ lại công thức tính chu vi hình vuông. Nếu độ dài cạnh của hình vuông được biểu diễn bằng S thì chu vi bằng bốn lần độ dài cạnh đó, tức là P = 4s.

Bước 2: Tìm độ dài cạnh của hình vuông, rồi nhân nó với 4. Tùy theo bài toán cụ thể, bạn có thể đo độ dài cạnh bằng thước, hoặc tham khảo thông tin của đề bài để biết độ dài cạnh của hình vuông. Đây là vài ví dụ:

Nếu độ dài một cạnh của hình vuông là 4 thì P = 4 * 4, tức là 16.

Nếu độ dài một cạnh của hình vuông là 6 thì P = 4 * 6, là 24.

Phương pháp tính chu vi hình vuông khi chỉ biết diện tích của hình vuông đó.

Bước 1: Hiểu công thức về diện tích hình vuông. Diện tích hình chữ nhật (hình vuông là hình chữ nhật đặc biệt) bằng chiều dài nhân với chiều rộng. Vì chiều dài và chiều rộng của hình vuông bằng nhau nên diện tích của hình vuông có độ dài cạnh s là s * s, nghĩa là A = s2.

Bước 2: Tìm căn bậc hai của diện tích. Căn bậc hai của diện tích là độ dài cạnh của hình vuông. Đối với hầu hết các số, bạn cần một máy tính để tìm căn bậc hai của nó. Nhập số trên máy tính trước, sau đó nhấn phím căn bậc hai (√) để lấy căn bậc hai của số đó. Bạn cũng có thể học cách tính căn bậc hai bằng tay.

Nếu diện tích là 20, thì độ dài cạnh s = √20, là 4,472.

Nếu diện tích là 25, thì độ dài cạnh s = √25, là 5.

Bước 3: Nhân chiều dài cạnh với 4. Sử dụng độ dài cạnh s mà bạn vừa tính được và thay nó vào công thức tính chu vi P = 4s. Kết quả cuối cùng là chu vi của hình vuông.

Ví dụ: Cho một hình vuông có diện tích là 20 và chiều dài cạnh là 4,472, chu vi là P = 4 * 4,472, là 17,888.

Đối với một hình vuông có diện tích là 25 và độ dài cạnh là 5, chu vi là P = 4 * 5, là 20.

Phương pháp tính chu vi hình vuông nội tiếp đường tròn

Trước hết cần hiểu thế nào là đường tròn nội tiếp hình vuông. Trong các kỳ thi GMAT và GRE thường xuất hiện khái niệm này nên cần hiểu rõ khái niệm. Hình vuông nội tiếp đường tròn là hình vuông được vẽ trong đường tròn và bốn đỉnh của hình vuông đều nằm trên chu vi.

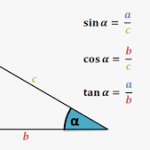
Hiểu mối quan hệ giữa bán kính của hình tròn và độ dài cạnh của hình vuông. Khoảng cách từ tâm của hình tròn đến một góc bất kỳ của hình vuông là bán kính của hình tròn. Để tìm độ dài cạnh s, ta cần tưởng tượng rằng hình vuông được cắt theo đường chéo thành hai tam giác vuông, mỗi tam giác có độ dài cạnh góc vuông bằng a, b và cạnh huyền c, cạnh huyền chiều dài bằng bán kính của hình tròn. Hai lần bằng 2r.

Sử dụng Định lý Pitago để tìm độ dài cạnh của hình vuông. Định lý Pitago mô tả mối quan hệ giữa hai cạnh góc vuông a và b của tam giác vuông và cạnh huyền c, nghĩa là a2 + b2 = c2. Vì a và b bằng nhau (chúng ta tính được một bình phương) và c = 2r, chúng ta có thể liệt kê các phương trình cần giải:

a2 + a2 = (2r) 2, để đơn giản hóa: 2a2 = 4 (r) 2, chia cả hai vế cho 2: (a2) = 2 (r) 2, hình vuông cả hai cạnh: a = √ (2r). Độ dài cạnh s là √ (2r).

Nhân chiều dài cạnh với 4. Trong ví dụ này, chu vi của hình vuông P = 4√ (2r). Theo luật phân phối, 4√ (2r) bằng 4√2 * √r, do đó ta có thể thay trực tiếp vào phương trình sau: P = 5.657r, trong đó r là bán kính của đường tròn ngoại tiếp.