SỐ CHÍNH PHƯƠNG là gì (đầy đủ)

Số chính phương là gì

Trong toán học, một số chính phương hay bình phương hoàn hảo là một số nguyên là bình phương của một số nguyên; nói cách khác, nó là tích của một số nguyên với chính nó. Ví dụ, 9 là một số bình phương, vì nó bằng 3^2 và có thể được viết dưới dạng 3 × 3.

Kí hiệu thông thường cho bình phương của một số n không phải là tích n × n, mà là lũy thừa tương đương n^2, thường được phát âm là “n bình phương”. Tên hình vuông bắt nguồn từ tên của hình dạng. Đơn vị diện tích được định nghĩa là diện tích của một hình vuông đơn vị (1 × 1). Do đó, một hình vuông với độ dài cạnh n có diện tích n^2. Nói cách khác, nếu một số bình phương được biểu diễn bởi n điểm, thì các điểm có thể được sắp xếp thành hàng như một hình vuông mỗi cạnh của chúng có cùng số điểm với căn bậc hai của n; do đó, số bình phương là một loại số tượng hình (các ví dụ khác là số lập phương và số tam giác).

Số chính phương không âm. Một cách khác để nói rằng một số nguyên (không âm) là một số bình phương là căn bậc hai của nó lại là một số nguyên.
Một số nguyên dương không có ước số chính phương hoàn hảo ngoại trừ 1 được gọi là không bình phương.

Đối với số nguyên không âm n, số chính phương thứ n là n^2, với 02 = 0 là số 0. Khái niệm bình phương có thể được mở rộng cho một số hệ thống số khác. Nếu bao gồm các số hữu tỉ, thì một bình phương là tỉ số của hai số nguyên bình phương và ngược lại, tỉ số của hai số nguyên bình phương là một số chính phương.

Hợp số la gì

Một số tổng hợp là một số nguyên dương có thể được tạo thành bằng cách nhân hai số nguyên dương nhỏ hơn. Tương tự, nó là một số nguyên dương có ít nhất một ước số khác 1 và chính nó. Mọi số nguyên dương đều là hợp số, số nguyên tố hoặc đơn vị 1, vì vậy các số tổng hợp chính xác là các số không phải là số nguyên tố và không phải là đơn vị.

Ví dụ, số nguyên 14 là một số hợp vì nó là tích của hai số nguyên nhỏ hơn 2 × 7. Tương tự như vậy, số nguyên 2 và 3 không phải là hợp số vì mỗi số chỉ có thể chia cho một và chính nó.

Các số tổng hợp lên đến 150 là

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140, 141, 142, 143, 144, 145, 146, 147, 148, 150. (trình tự A002808 trong OEIS)
Mọi số tổng hợp có thể được viết dưới dạng tích của hai hoặc nhiều số nguyên tố (không nhất thiết phải khác biệt). Ví dụ, số hỗn hợp 299 có thể được viết là 13 × 23 và số tổng hợp 360 có thể được viết là 23 × 32 × 5; hơn nữa, biểu diễn này là duy nhất theo thứ tự của các yếu tố. Thực tế này được gọi là định lý cơ bản của số học.
Có một số phép thử tính nguyên thủy đã biết có thể xác định xem một số là số nguyên tố hay hợp số mà không nhất thiết phải tiết lộ thừa số của đầu vào tổng hợp.

Một cách để phân loại hợp số là đếm số thừa số nguyên tố. Một số tổng hợp có hai thừa số nguyên tố là bán chuẩn hoặc gần như nguyên tố (các thừa số không cần phân biệt, do đó bình phương của các số nguyên tố được bao gồm). Một số hợp với ba thừa số nguyên tố phân biệt là một số hình cầu. Trong một số ứng dụng, cần phân biệt các hợp số với một số lẻ thừa số nguyên tố riêng biệt và những hợp số có một số chẵn thừa số nguyên tố phân biệt.
Nếu tất cả các thừa số nguyên tố của một số được lặp lại thì nó được gọi là số mạnh (Tất cả các lũy thừa hoàn hảo đều là số mạnh). Nếu không có thừa số nguyên tố nào của nó được lặp lại, nó được gọi là không bình phương. (Tất cả các số nguyên tố và 1 đều là số không bình phương.)

Ví dụ, 72 = 23 × 32, tất cả các thừa số nguyên tố đều được lặp lại, do đó 72 là một số mạnh. 42 = 2 × 3 × 7, không có thừa số nguyên tố nào được lặp lại, do đó 42 là không bình phương.

Biểu đồ Euler của các số dồi dào, nguyên thủy, dồi dào, dư thừa, khổng lồ, nhiều tổng hợp, tổng hợp cao cấp, các số kỳ lạ và hoàn hảo dưới 100 liên quan đến số thiếu và tổng hợp
Một cách khác để phân loại số hợp là đếm số ước. Một số n có nhiều ước hơn bất kỳ x <n nào là một số có tổng số cao (mặc dù hai số đầu tiên như vậy là 1 và 2).

Các số tổng hợp cũng đã được gọi là “số hình chữ nhật”, nhưng tên đó cũng có thể đề cập đến các số pronic, các số là tích của hai số nguyên liên tiếp.

Tuy nhiên, một cách khác để phân loại số tổng hợp là xác định xem tất cả các thừa số nguyên tố đều nằm dưới hoặc nằm trên một số cố định (nguyên tố) nào đó. Những con số như vậy được gọi là số trơn và số thô, tương ứng.

Số chính phương C++

Ở đây chúng ta có thể đánh số bình phương bằng cách sử dụng hàm Power. Bạn sẽ cần bao gồm #include <cmath> cho nó. Bên trong hàm, chúng ta cần chuyển giá trị Cơ sở mà chúng ta muốn bình phương và giá trị Nguồn (đối với hình vuông, nó sẽ là 2). Vì vậy, ví dụ sẽ là Pow (Power, Base). Bạn có thể coi nó như một toán tử bình phương c ++.

Số chính phương nhỏ hơn 100

Số chính phương nhỏ hơn 100 bao gồm 0, 1, 4, 9, 16, 25, 36, 42, 64, 81.

Số chính phương là gì
Kiểm tra số chính phương
Liệt kê các số chính phương
Số chính phương nhỏ nhất

Cách tìm số chính phương

(1) Nhân hai số âm cũng sẽ được một số dương. Do đó, (-5) * (- 5) cũng bằng 25. Vì vậy, -5 cũng là căn bậc hai của 25. Nhưng nói chung, chúng ta giả sử căn bậc hai của một số dương là một số dương.

(2) Căn bậc hai của 1 luôn bằng 1.

Chúng ta biểu diễn căn bậc hai của một số bằng dấu căn (√). Ví dụ: √36 = 6 (vì 6 x 6 = 36)

Ghi chú:

(3) Tìm căn bậc hai của một số âm (tức là khi dấu âm nằm bên trong dấu căn, tức là √-36) hơi phức tạp và không phù hợp với bài viết này.

(4) nếu dấu trừ được cho bên ngoài dấu căn (tức là -√36), thì câu trả lời sẽ luôn là -6.

 

Có hai loại số:

Các số là một bình phương hoàn hảo: Tích của một số nguyên với chính nó. Ví dụ: 9 * 9 = 81.

Các số là một bình phương không hoàn hảo: Nhân bất kỳ số nào với chính nó. Ví dụ: 2,236 * 2,236 = 5.

Tìm căn bậc hai của một số bình phương không hoàn hảo khó hơn một chút so với việc tìm căn bậc hai của một số bình phương hoàn hảo. chúng ta sẽ đề cập đến cả hai chủ đề trong bài viết cụ thể này. Nhưng trước đó, chúng ta phải hiểu căn bậc hai được dùng để làm gì.

Ví dụ, Rhea đang tìm một căn hộ ở Delhi. Cô ấy đang tìm kiếm một căn hộ 2 phòng ngủ, nơi cô ấy có thể sống với em gái của mình. Một vài cuộc điện thoại sau đó, cô ấy đã chọn được hai địa điểm sau khi nhìn thấy hình ảnh của họ trên mạng. Một là 1600 mét vuông với một ban công và kia là 2500 mét vuông với hai ban công. Giờ đây, cô có thể dễ dàng đo kích thước của căn hộ đầu tiên là 40 feet x 40 feet. Căn hộ thứ hai sẽ là 50 feet x 50 feet. Đây chỉ là một ví dụ. Căn bậc hai được sử dụng cho nhiều mục đích như thế này.

 

Bây giờ đến với chủ đề chính của chúng ta, tức là làm thế nào để tìm căn bậc hai của một số?

(A) Số Vuông Hoàn hảo: –
Trước khi tìm căn bậc hai của một số, chúng ta phải biết bình phương của 9 số tự nhiên đầu tiên.

1 * 1 = 1

2 * 2 = 4

3 * 3 = 9

4 * 4 = 16

5 * 5 = 25

6 * 6 = 36

7 * 7 = 49

8 * 8 = 64

9 * 9 = 81

Từ biểu đồ trên, chúng ta có thể kết luận như sau:

Một bình phương hoàn hảo không thể có 2, 3, 7 hoặc 8 trong chữ số của hàng đơn vị.

Nếu một bình phương hoàn hảo kết thúc bằng 1, thì chữ số hàng đơn vị của căn bậc hai của nó phải là 1 hoặc 9.

Nếu một bình phương hoàn hảo kết thúc bằng 4, thì chữ số hàng đơn vị của căn bậc hai của nó phải là 2 hoặc 8.

Nếu một bình phương hoàn hảo kết thúc bằng 5, thì chữ số hàng đơn vị của căn bậc hai của nó chắc chắn là 5.

Nếu một bình phương hoàn hảo kết thúc bằng 6, thì chữ số hàng đơn vị của căn bậc hai của nó phải là 4 hoặc 6.

Nếu một bình phương hoàn hảo kết thúc bằng số 9, thì chữ số hàng đơn vị của căn bậc hai của nó phải là 3 hoặc 7.

 

Lưu ý: Đầu tiên, chúng ta phải tìm ra số chữ số trong câu trả lời.

Căn bậc hai của một số có số chữ số lẻ (ví dụ: 24563 có 5 chữ số tức là số lẻ) sẽ có (n + 1) / 2 chữ số trong câu trả lời (trong ví dụ của chúng ta, (5 + 1) / 2 = 3 chữ số trong câu trả lời).

Căn bậc hai của một số có một số chữ số chẵn (ví dụ: 2456 có 4 chữ số tức là chẵn) sẽ có n / 2 chữ số trong câu trả lời (trong ví dụ của chúng ta, 4/2 = 2 chữ số trong câu trả lời).

 

chúng ta sẽ hiểu các bước tiếp theo với sự trợ giúp của một ví dụ. Giả sử, chúng ta phải tìm ra căn bậc hai của 2116.

(1) Số chữ số trong câu trả lời của chúng ta sẽ là 4/2 = 2

(2) chúng ta sẽ chia 2116 thành 2 nhóm. 21 và 16.

Lưu ý: Nếu chúng ta lấy một số có 3 chữ số như 121, chúng ta sẽ coi là 01 và 21. Tương tự, nếu chúng ta lấy một số có năm chữ số như 11025, chúng ta sẽ coi là 110 và 25. Điều này cho thấy rằng thứ hai cặp phải luôn chỉ có hai chữ số cuối cùng.

(3) bình phương gần nhất với cặp đầu tiên, tức là 21 là 16 và 25. chúng ta sẽ luôn lấy bình phương nhỏ hơn. Căn bậc hai của 16 là 4. Vậy chữ số đầu tiên của câu trả lời cuối cùng là 4.

(4) Bây giờ chúng ta hãy đến với cặp thứ hai, tức là 16. Kiểm tra chữ số của đơn vị. Trong trường hợp của chúng ta, nó là 6 có nghĩa là căn bậc hai là 4 hoặc 6 như đã đề cập trong mô tả. Vì chữ số đầu tiên của căn bậc hai là 4 và chúng ta biết rằng đó là số có hai chữ số, căn bậc hai của 2116 có thể là 44 hoặc 46. Con số này nằm trong khoảng từ 40 đến 50.

(5) Tiếp theo, ta phải vuông 40 và 50, ta được 1600 và 2500 tương ứng.

(6) Tìm ra con số nào trong số những con số này gần với câu hỏi đã cho. Trong trường hợp của chúng ta, 2116 gần với 50. Do đó, căn bậc hai của 2116 là 46.

Thực hành thường xuyên có thể giúp bạn thực hiện các bước này một cách nhanh chóng.

 

Tính chất số chính phương

Một số có 2, 3, 7 hoặc 8 ở vị trí của đơn vị sẽ không bao giờ là một số chính phương. Nói cách khác, không có số bình phương nào kết thúc bằng 2, 3, 7 hoặc 8.
Nếu số không ở cuối là số chẵn, thì số đó là một số chính phương. Nếu không, chúng ta có thể nói rằng số kết thúc bằng một số lẻ các số không không bao giờ là một số chính phương
Nếu các số chẵn bình phương, nó luôn cho kết quả là các số chẵn. Ngoài ra, nếu các số lẻ được bình phương, nó luôn cho các số lẻ.
Nếu các số tự nhiên khác một được bình phương, thì nó phải là bội của 3 hoặc vượt quá bội của 3 với 1.
Nếu các số tự nhiên khác một được bình phương, nó phải là bội số của 4 hoặc vượt quá bội số của 4 x 1.
Cần lưu ý rằng chữ số hàng đơn vị của bình phương một số tự nhiên bằng chữ số hàng đơn vị của bình phương chữ số ở vị trí hàng đơn vị của số tự nhiên đã cho.
Có n số tự nhiên, viết p và q sao cho p 2 = 2q 2
Với mọi số tự nhiên n, ta có thể viết thành: (n + 1) 2 – n 2 = (n + 1) + n.
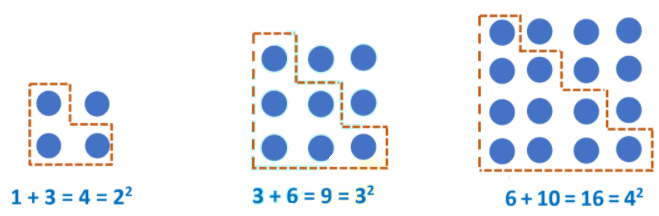
Nếu một số n bình phương thì nó bằng tổng của n số tự nhiên lẻ đầu tiên.
Với bất kỳ số tự nhiên nào, giả sử “n” lớn hơn 1, chúng ta có thể nói rằng (2n, n 2 – 1, n 2 + 1) phải là một bộ ba Pitago.