Hỏi bài tập và công thức tính diện tích Lục giác, Lục giác đều

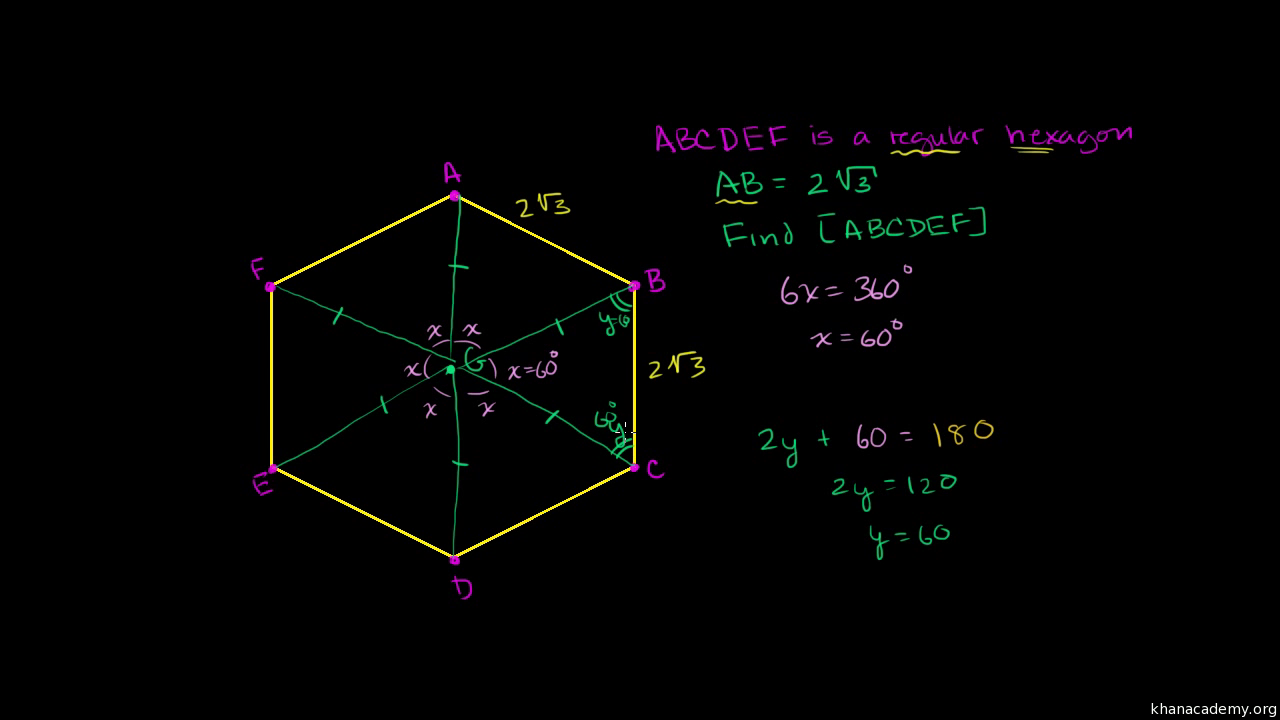
Hình lục giác là hình đa giác có sáu cạnh và góc. Hình lục giác đều có sáu cạnh và góc bằng nhau và được tạo bởi sáu tam giác đều. Có nhiều cách để tính diện tích của một hình lục giác, cho dù bạn đang làm việc với một hình lục giác không đều hay một hình lục giác đều. Nếu bạn muốn biết cách tính diện tích của một hình lục giác, chỉ cần làm theo các bước sau.

Tính toán từ một hình lục giác đều với độ dài cạnh cho trước

Bước 1
Viết công thức tính diện tích hình lục giác nếu bạn biết độ dài cạnh. Vì một lục giác đều bao gồm sáu tam giác đều, nên công thức tính diện tích của một lục giác được suy ra từ công thức tìm diện tích của một tam giác đều. Công thức tìm diện tích của một lục giác là Diện tích = (3√3 s2) / 2 trong đó s là độ dài một cạnh của lục giác đều.

Bước 2
Xác định độ dài của một cạnh. Nếu bạn đã biết độ dài của một cạnh, thì bạn có thể viết nó ra đơn giản; trong trường hợp này, chiều dài của một cạnh là 9 cm. Nếu bạn không biết độ dài của một cạnh nhưng biết độ dài của chu vi hoặc cạnh (chiều cao của một trong các tam giác đều do lục giác tạo thành, vuông góc với mặt bên), bạn vẫn có thể tìm được độ dài của mặt của hình lục giác. Đây là cách bạn làm điều đó:
Nếu bạn biết chu vi, sau đó chỉ cần chia nó cho 6 để có được độ dài của một cạnh. Ví dụ, nếu chiều dài của chu vi là 54 cm, sau đó chia nó cho 6 để được 9 cm, chiều dài của cạnh.
Nếu bạn chỉ biết ô vuông, bạn có thể tìm độ dài của một cạnh bằng cách cắm ô vuông vào công thức a = x√3 và sau đó nhân câu trả lời với hai. Điều này là do apothem đại diện cho cạnh x√3 của tam giác 30-60-90 mà nó tạo ra. Ví dụ: nếu apothem là 10√3, thì x là 10 và độ dài của một cạnh là 10 * 2 hoặc 20.

Bước 3
Thêm giá trị của độ dài cạnh vào công thức. Vì bạn biết rằng độ dài một cạnh của tam giác là 9, chỉ cần thêm 9 vào công thức ban đầu. Nó sẽ như thế này: Diện tích = (3√3 x 92) / 2

Bước 4
Đơn giản hóa câu trả lời của bạn. Tìm giá trị của phương trình và viết đáp số. Vì bạn đang làm việc với diện tích, bạn nên nêu câu trả lời của mình theo đơn vị hình vuông. Đây là cách bạn làm điều đó:
(3√3 x 92) / 2 =
(3√3 x 81) / 2 =
(243√3) / 2 =
420,8 / 2 =
210,4 cm2

Tính toán từ một hình lục giác đều với một Apothem cho trước

Bước 1
Viết công thức tính diện tích của một lục giác có một cạnh cho trước. Công thức đơn giản là Diện tích = 1/2 x chu vi x apothem. [3]

Bước 2
Viết ra lời mai. Giả sử apothem là 5√3 cm.

Bước 3
Sử dụng apothem để tìm chu vi. Vì apothem vuông góc với cạnh của hình lục giác nên nó tạo ra một cạnh của hình tam giác 30-60-90. Các cạnh của hình tam giác 30-60-90 theo tỷ lệ xx√3-2x, trong đó chiều dài của chân ngắn, đối diện với góc 30 độ, được biểu thị bằng x, chiều dài của chân dài, nằm đối diện với góc 60 độ, được biểu thị bằng x√3 và cạnh huyền được biểu thị bằng 2x.
Apothem là cạnh được đại diện bởi x√3. Do đó, hãy cắm độ dài của apothem vào công thức a = x√3 và giải. Ví dụ, nếu chiều dài của apothem là 5√3, hãy cắm nó vào công thức và nhận được 5√3 cm = x√3, hoặc x = 5 cm.
Bằng cách giải cho x, bạn đã tìm được độ dài của cạnh ngắn của tam giác, 5. Vì nó đại diện cho một nửa độ dài của một cạnh của hình lục giác, hãy nhân nó với 2 để có độ dài đầy đủ của cạnh đó. 5 cm x 2 = 10 cm.
Bây giờ bạn biết rằng độ dài của một cạnh là 10, chỉ cần nhân nó với 6 để tìm chu vi của hình lục giác. 10 cm x 6 = 60 cm

Bước 4
Đưa tất cả các đại lượng đã biết vào công thức. Phần khó nhất là tìm chu vi. Bây giờ, tất cả những gì bạn phải làm là thêm apothem và chu vi vào công thức và giải:
Diện tích = 1/2 x chu vi x apothem
Diện tích = 1/2 x 60 cm x 5√3cm